《计算方法》实验四插值法

一、实验目的：

掌握拉格朗日插以及多项式插值的震荡问题

二、实验任务：

考虑一个固定的区间上用插值逼近一个函数。显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。我们自然关心插值多项式的次数增加时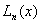，是否也更加靠近被逼近的函数。龙格（Runge）给出一个例子是极著名并富有启发性的。设区间[-1,1]上函数

三、实验内容：

考虑区间[-1,1]的一个等距划分，分点为

则拉格朗日插值多项式为

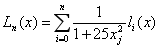
其中的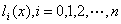是n次拉格朗日插值基函数。

四、上机习题：

（1） 选择不断增大的分点数目n=2,3….，画出原函数f(x)及插值多项式函数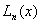在[-1，1]上的图像，比较并分析实验结果。

（2）选择其他的函数，例如定义在区间[-5，5]上的函数

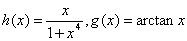
重复上述的实验看其结果如何。

（3）区间[a,b]上切比雪夫点的定义为

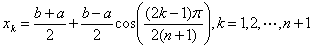
以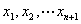为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果。